Click logo to return to 'links-page'

• Source-code - the perfect rationality of 'Stringularity' leads to the perfect irrationality of 'Phi'.
• Stringularity is trinitarian (3 in 1) and self-referential i.e it appeals to nothing beyond itself.
  
  
• As this is a 'singularity' the observer & the observed are one.
• As this precedes anything 'human', it is non-anthropomorphic.
  
  
• A perfect rationality that couples the 'perfect-irrationality' of 'Phi' and the transcendence of 'Pi' in the cosmological commons . . .
• Latent before and patent after the big bang, this is Nature's smallest and most beautiful secret - 'Force majeure'
  
  
• The order of the harmonic-series shows the basis of why these things can be said - it is what today we call a 'major chord'.
  
• Sympathetic-vibration to the harmonic-series is the empathy of cognitive-resonance around this fundamental order.
  
  
• Cognitive-dissonance arising with probability distributions between waves & particles certainly obscures this. However,
  
• Cognitive-consonance arising between wave-rates-ratios simply precedes this, as explored David Bohm's The Implicate Order.
  
  ***********************************************
  
  Vibrating Strings
  
  ***********************************************
  
  
  

The rate of vibration heard covers three 'octaves' in super-position, through 100 Hz, 200 Hz, 300 Hz, 400 Hz, 500 Hz, 600 Hz, 800 Hz, revealing pure harmony.
The rate of vibration seen is slowed down by a factor of 100 so it can actually be seen in detail rather than as a 'blur' at real-time speed (Hz measure space-time).

This phenomenon is neither 'top-down' nor 'bottom-up'. It is true at all scales of all dimensions.
It leads directly to well-tempering and the 'Well Tempered Climate Accord' (WTCA).
The universe is impossible without 'Phi' and 'Phi' derivation is impossible without Well Tempering.
Conclusion: Nature itself is well tempered and so paradoxically, both rational and irrational.

*************************************************************

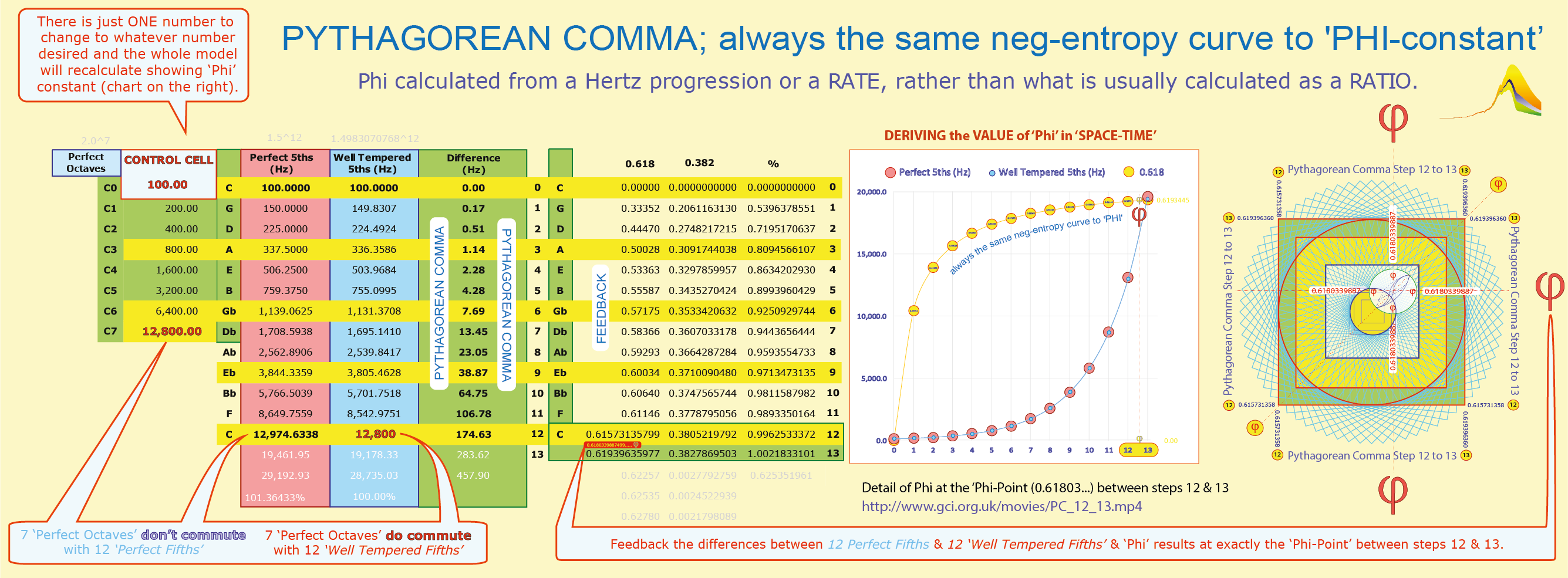
The calculating spreadsheet for this Phi-Derivation model is down-loadable here
High or low, whatever value is entered by the user in the 'Control Cell', the Phi curve always remains the same.

The value of Phi emerges as a universal-constant at exactly the Phi-Point between steps 12 &13 of the Pythagorean Comma
regardless of the base number entered by the user.



************************************************************************

The ‘Stringularity’ Hypothesis

How Pythagoras' simple string experiment, conducted in Crotone around 530 BC,
embeds a per-unit-time-based-derivation of the beautiful and irrational 'Phi'.

************************************************************************

The value of ‘Phi’ (.618…) is irrational. It is commonly derived from a ‘quadratic equation’
((the square root of 5 + 1)/2) or the Fibonacci Series (as in the Pentagon:Pentangle).

However, the value of ‘Phi’ can be quantized per-unit-time (Hz) from measuring and back-feeding
the differences in the phenomenon known as the ‘Pythagorean Comma’. Derived from ‘Stringularity’,
‘Phi’ is a point on a curve at the ‘Phi-point’, between steps 12 and 13 of the Pythagorean Comma.

It is constant, anywhere from nano-to-macroscale. So, using the derivation of ‘Phi’ as a function of
steps per-unit-time, can be a relevant step in changing the cognitive paradigm where particles in
wave-fields are only probability perceptions still regarded as the ‘quantum measurement problem’.

********************************************************************

The ‘Stringularity’ Hypothesis; the ‘path-integral’ of Pythagoras’ String Experiment

The now famous string experiment of Pythagoras (~ 530 BCE) demonstrates that: -

1. When we take a string of constant length and constant tension tuned at 100 Hz
2. And halve the length of the string, the frequency (Hz) doubles from 100 Hz to 200 Hz
3. And that if we third the length of the string the frequency (Hz) trebles to 300 Hz etc . . . .

As the path-integral basis of the universally constant ‘harmonic series’, these steps start with: -

1. the ‘Fundamental’
2. the ‘Perfect Octave’
3. the ‘Perfect Octave plus the Perfect Fifth’ etc . . .
   sub-division by any rational number will produce a 'harmonic' in this series . . . .

The Pythagorean Comma (see chart above)

Proceeding from above, the Pythagorean Comma emerges as a growing ‘gap’: -

1. when we sequence seven ‘Perfect Octaves’ in Hertz (Hz), in the example shown we go through
   seven doublings 1 (each enlarging by 200%), from 100 Hz to 12,800.00 Hz,
   
   
2. when we sequence twelve ‘Perfect Fifths’ we go in the example shown we go through 12 steps
   (each enlarging by 150%) from 100 Hz to 12,974.63 Hz,
   
   
3. it becomes clear that seven Perfect Octaves (12,800.00 Hz) do not ‘commute’ exactly with
   twelve ‘Perfect Fifths’ 12,974.63 Hz. At this ‘twelfth-step’, the gap is 174.63 Hz (1.345...%)

Well-Tempered Tuning (see chart above)

1. In order to get the twelve Perfect Fifths to commute with the seven Perfect Octaves,
   the Perfect Fifths (enlarging at 150%) are ‘Well Tempered’, enlarging at 149.83070768…%)
   
   
2. The result of adopting this procedure is that twelve Well-Tempered Fifths commute exactly
   with seven Perfect Octaves (at 12,800 Hz), giving rise to what is called 'Well Tempered Tuning' (3, 4,)
   

The Hz Differences between Perfect and Well-Tempered Fifths lead to ‘Phi’

1. When step-by-step, we subtract 12 Well Tempered Fifths from 12 Perfect Fifths,
   a sequence of differences between the two paths is the result (see table above),
   
   
2. When step-by-step, we back feed these differences into the sequence, so the largest
   difference is divided into the smaller difference that precedes it etc . . . (see table above),
   
   
3. A twelve step sequence with negative curvature (concavity) is revealed, decreasing from
   0.615731…. just below the value of ‘Phi’, to 0.000 (see table above),
   
   
4. When we go one step further and start at the thirteenth step of the Pythagorean Comma,
   the difference is 283.62 Hz, yielding a value 0.6199396…. just above the value of ‘Phi.

‘Phi’ is exactly at the Phi-Point between per-unit-time steps 12 & 13 of the Pythagorean Comma

1. The value of ‘Phi’ is on the overall curve at exactly the Phi-point between steps 12 and 13
   of the Pythagorean Comma http://www.gci.org.uk/movies/PC_12_13.mp4
   
   
2. Exponential growth curves at 200% 150% and 149.83070768…% etc are positively governed
   by acceleration (convexity) and unfold without limit towards infinity.
   
   
3. Path-integral to that, the growth curve to ‘Phi’, is governed by deceleration within the
   feedback limits or concavity that define it, countervailing the convexity of acceleration.
   
   
4. Deriving the value of ‘Phi’ from measuring the path-integral per-unit-time/space of
   ‘Stringularity’ is distinct from the time-free quadratic equation and Fibonacci Series.
   
   
5. This path-integral procedure gives rise to an array of time-based features which suggest corroboration.

The beauty and the deceptive simplicity of ‘Phi’ underlies the structure, the sequencing,
the symmetry and the curvature of natural phenomena, from the nanoscale to the macroscale.

Could this 'musical-derivation' of ‘Phi’ be a simple yet beautiful idea that helps to answer Erwin Schrodinger’s
famous question, ‘What is Life’? Might it underlie a ‘cognitive framework’ that would help better to understand
the wave:particle perceptions-dichotomy, the path-integral complexity, the moment:momentum continuity and
life:death challenges that will always face us?