• Having played in and written for symphony orchestras for much of the last 70 years, it seems helpful to present this user-chooser audio-visual animations
  demonstrating Pythagoras’ law of stringularity. This is a universal constant, recognized by Pythagoaras ~530 BC. It demonstrates audio-visually like this
  
  
  

The rate of vibration heard covers three 'octaves' in super-position, through 100 Hz, 200 Hz, 300 Hz, 400 Hz, 500 Hz, 600 Hz, 800 Hz, revealing pure harmony.
The rate of vibration seen is slowed down by a factor of 100 so it can actually be seen in detail rather than as a 'blur' at real-time speed (Hz measure space-time).

This phenomenon is neither 'top-down' nor 'bottom-up'. It is true at all scales of all dimensions. It leads directly to well-tempering and the 'Well Tempered Climate Accord' (WTCA).
Music - the universe itself - is impossible without this. Equally UNFCCC-Compliance is impossible without WTCA. "This is not just the 'right way, it is the only way" (GLOBE Point 16)

***************************************************************************

Pythagoras Law

***************************************************************************

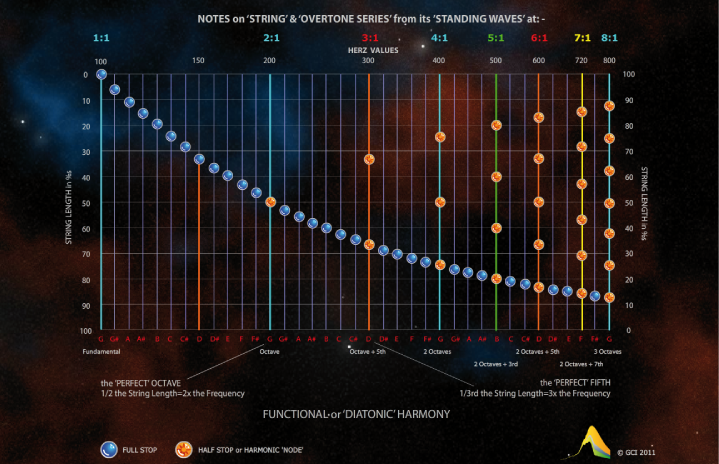
Pythagoras’ ‘law’ is revealed in a string at constant tension and length, as in the cello G-String shown here for example. The image has Hz values based on G'0'=100 Hz, which is equivalent to a Cello G-String. Here, Herz values have been slowed visually by a factor of 100, so the Herz doubling for the octave and trebling for the fifth [etc] can more easily be ‘seen’ as well as 'heard' [as 'doublings', treblings' etc].

Click on the strings-picture below to animate as an andio-visual with user controls.
The audio-visual file for this is also here.

Once in the animation, mouse-touching buttons [one click ‘on’, second click ‘off’] AV animates each string.
The user controls of the animation enable any combination-progression within octave:12 semi-tone 'tonality'.

The sounds and sights of harmonic progressions are a click away.

• The gold-coloured buttons in the image to both hear and see how the ‘harmonics’ of the whole string, or the ‘overtone series’, emerges ‘harmoniously’ from the ‘fundamental’ G.
• The blue-coloured buttons for ‘chromatic’ notes in between are not ‘harmonics’ in the first three octave, but as whole numbers become harmonics in higher octaves.
  
  
  
  Here is a little more on the derivation and significance of 'Phi'
  
  From zero to one; so what really happened at the Big Bang?
  
  

***************************************************************************

Hemiola - the most under-estimated figures in history

***************************************************************************

With stringularity the first three steps are the Hemiola (1:2:3).
Here is the most famous Hemiola in all the musical repertoire - it is from 'Thus Spake Zarathustra' by Richard Strauss.