Music & Nature's derivation of 'Phi'; the 'divine rate' at the heart of organic growth
Click logo to return to 'links-page'
Welcome to find that this web-page on 'Music & Nature's derivation of Phi' is
cited here in 'Fine-Structure Constant from Golden Ratio Geometry' as follows: -
by Michael A. Sherbon
a mathematician and musician at
Case Western Reserve University Alumnus
January 24, 2018
and referenced again here
Concerning_Musical_Tuning_the_Fibonacci.pdf

**********************************************
A user-chooser Phi at any scale 'calculator' is here
**********************************************
Since writing the web-page below I have: -
- plotted the position of the Fine Structure Constant (FSC) on the Phi-Curve as here and here and here and
- made a short movie showing the eigen-value structure-sequence of the harmonic series and the Phi-Curve . . . .

However, the constancy of this much measured constant is speculated as as 'semi-constant' according to the time and distance
of measurement in a paper 'Does the fine structure constant vary with time and distance?'
**********************************************
This simple & beautiful mathematical truth is not in conflict with the basis of any religion or of any reputable science, humanist or otherwise.
If anything it suggests that at a seminal level, the dichotomy between science and religion (created by humans) is false . . . .
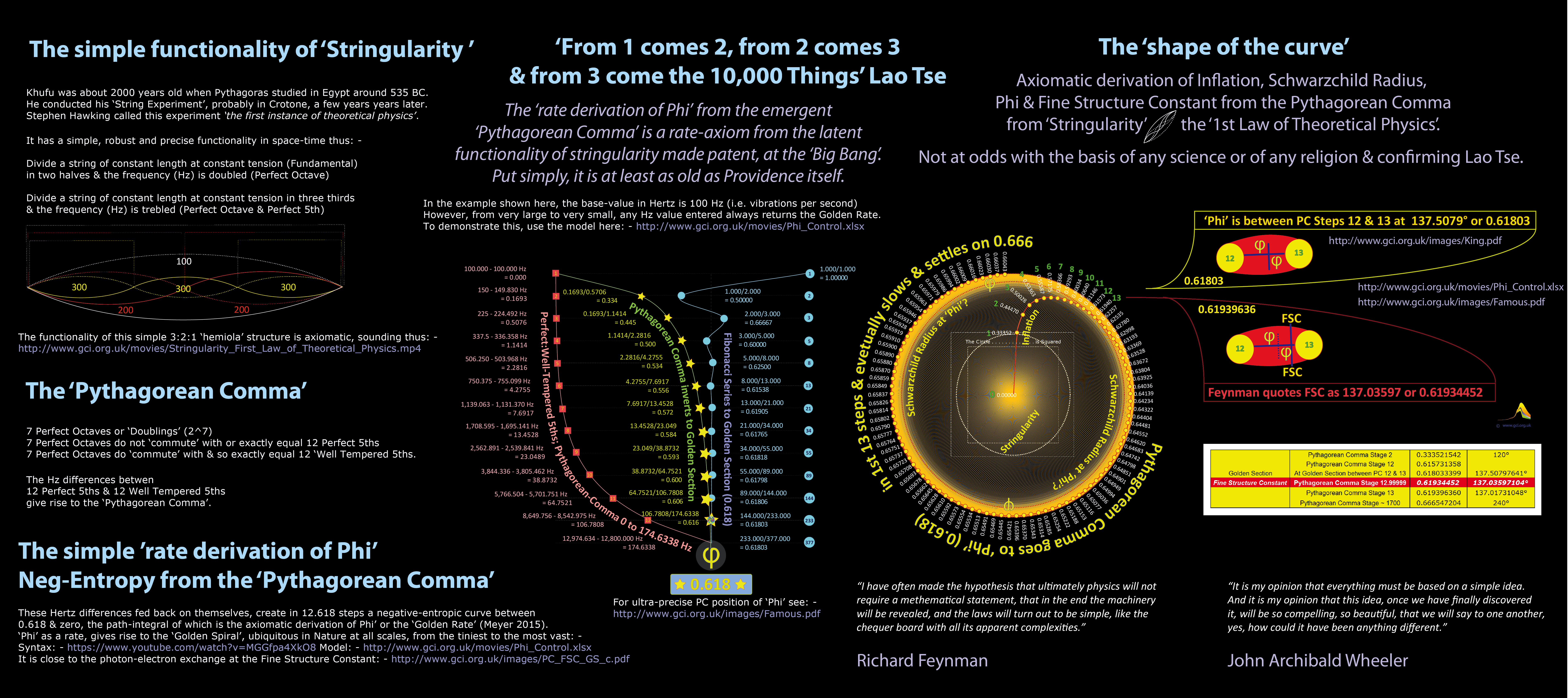
The 3-2-1 'Hemiola' - a Trinity of Wholeness - the First Law of Theoretical Physics
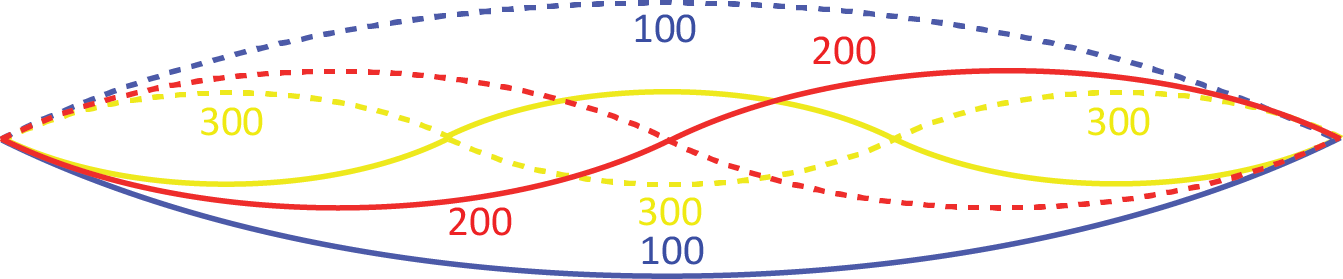
Pythagoras’ famous ‘string experiment’ from around 530 BCE, demonstrated relativity where: -
if a string of constant length and at constant tension vibrates at 1/1 it gives
One Fundamental @ 100 Hertz
if a string of constant length and at constant tension is divided into two 1/2 lengths, the rate at which each 1/2 vibrates doubles
& gives Two Perfect Octaves (with the fundamental this is the 'Tonic') @ 200 Hertz
if a string of constant length and at constant tension is divided into three 1/3 lengths,
the rate at which each 1/3 vibrates trebles & gives Three Perfect Fifths (with the 'tonic' this is the 'Dominant) @ 300 HertzTHREE, vibrating in the time of TWO, vibrating in the time of ONE, is called in music a ‘HEMIOLA’.
structured and sounding like this
Let us call this law 'Stringularity'
In 'stringularity the Fundamental, the Perfect Octave & the Perfect 5th are in a 'Tonic:Dominant' relationship'.
This combination gives rise to the basic functionality of music harmony, the 'Perfect Cadence' like an 'Amen' cadence, or where the dominant is drawn to resolve on the tonic.In 2010 particle physicist Stephen Hawking stated that we can call this, ‘the first instance of theoretical physics’.
In fact and in common with many other physicists who routinely cite Pythagoras, this acknowledgement draws well short of recognizing the profound structural implications of this 'instance'.The Derivation of Phi "Nature's most Beautiful & Best Kept Secret."
Stringularity also gives rise to 'Phi'. Given the universal significance of 'Phi', or the 'Golden Rate' (discussed in more detail below)
this 'Phi' derivation as a rate is simple, subtle and axiomatically obvious and yet it is still "Nature's smallest, most beautiful and best kept secret."
Here is a short audio/visual laying out these remarkable properties.'Stringularity' & 'Perfect Tuning'
In music this 'Stringularity' is quite simply the ‘First Law’. It gives rise to ‘Perfect’ or ‘Pythagorean Tuning’ where the intervals between the notes within the octave
being different for the seven tones and ‘semi-tones’ arising. This roots music played on an instrument that is tuned ‘Perfectly’, firmly in the key of the scale in which that instrument is tuned.In classical Greek music this procedure gave rise to the 7 'modes' (Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian & Locrian) each one starting on
a different one of the seven available notes in the scale, but while maintaining the order of the tones and semitones arising in the scale.Well Tempered Tuning
Around 2,225 years later ‘Equal Temperament’ or ‘Well-Tempered’ tuning was consolidated in Western music with J S Bach's ‘Well-Tempered Harpsichord’ (1722).
It eventually comprised the ‘48 Preludes & Fugues’ (four in each of the 12 keys available within the 'Perfect Octave') physically requiring ‘Equal Temperament’ or
‘Well Tempered Tuning’ of the Harpsichord - the tuning of each of the 12 semi-tones within the Octave was tuned so as to be in equal steps.
In both of these tuning systems a ‘Perfect Octave’ is always a ‘Perfect Doubling’ and this governs all tuning systems of the parts withing the octave.
In Well Tempered Tuning however, a ‘Perfect Fifth’ becomes a ‘Well Tempered Fifth’, comprised of seven of the 12 Well Tempered or ‘equal’ semi-tones within the 'Perfect Octave'.
In other words, this ‘Well Tempered Fifth’ becomes marginally smaller than the ‘Perfect Fifth’.
Well Tempered Tuning and the Pythagorean Comma
As the Bach Preludes & Fuges show, well-tempered tuning is a response to the Pythagorean Comma that roots the instrument equally
in any of the 12 keys available on each of the 12 semi-tones within the 'Perfect Octave'. It shows that music can be written in,
played in and modulate between any of the twelve ‘keys’ available within the 'Perfect Octave'.
As this remains 'in-tune', well-Tempered tuning remains the basis of Western music to this day.
Full three octave string user-chooser animation (audio/visual swf file - opens well in Firefox)
The Well Tempered Climate Accord
Like an orchestra playing in in tune and in time together, this Well-Tempered Climate Accord enables the carbon-contraction-budget to be ‘created and performed’
at whatever rate (or in whatever key) that science requires; in other words as a complete UNFCCC-Compliant 'event' (vide Adair Turner UK Climate Act).So the primary purpose of Well-Tempering the 'C&C' Climate Accord is practical and not ideological. It is so that any convergence rate to equal per capita rights can be negotiated,
while remaining an axiomatically self-structuring and self-limiting function of the global contraction-rate that the precautionary policy requires.
At root level this is governed by the stringularity law - here simply double the rate halve the weight.It reframes the randomness of the political-economic model employed to date to that purpose and continues to attract significant support for,
" . . . the virtue of simplicity; equal per capita emissions is a natural focal point where contestable computations based on economic variables do not need to enter the allocation formula."As a fundamental response to the requirements of compliance with the objective of the UN Framework Convention on Climate change, C&C continues to attract significant support.
The deeper significance of the Pythagorean Comma
The ‘Pythagorean Comma’ has a much greater significance than has yet been widely realised.
So at this point it is worth noting this foundational challenge coming quite separately from Richard Feynman and from John Archibald Wheeler.
The Pythagorean Comma axiomatically gives the derivation of 'Phi'
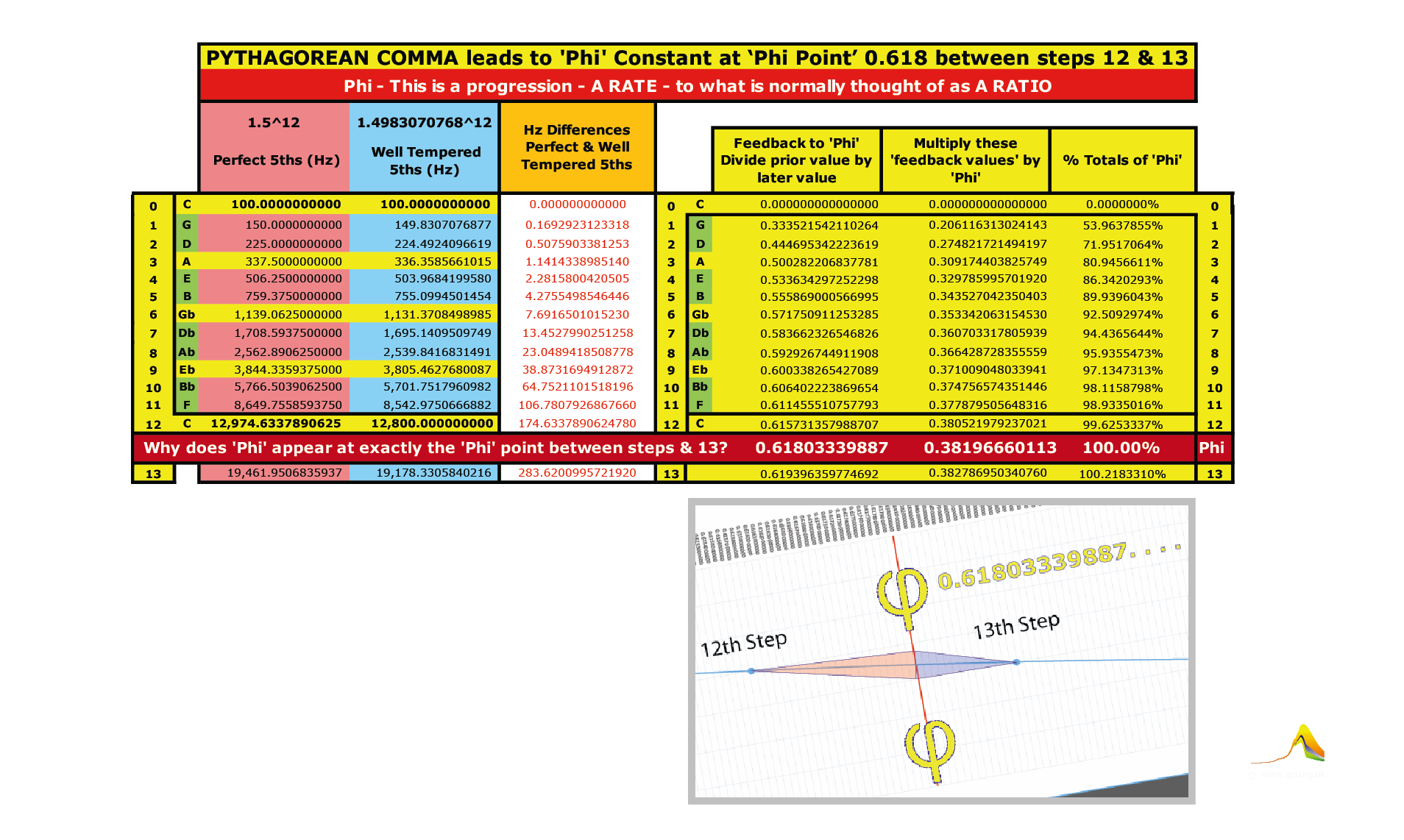
The 'Pythagorean Comma' is usually understood as a ‘gap’ that emerges between 2^7 (seven Perfect Octaves) compared with 1.5^12 (twelve Perfect Fifths);
in other words they don't quite 'commute'.However, when we progress the Hertz values through the sequence of 12 Well-Tempered 5ths (1.4983071^12) progressively diverging from twelve Perfect Fifths (1.5^12)
this exhibits the tiny deviations arising between 12 perfect fiths and 12 well tempered fifths. These are the key, as 7 Perfect Octaves do commute with 12 Well Tempered 5ths.
These deviations create a rising & widening Hertz differential. When this differential sequence of rate values is fed back on itself
(dividing the 12th value by the 13th, the 11th by the 12th etc) 'Phi' - but crucially also the derivation of 'Phi' - emerges.
In other words 'Phi' is a simple function of the first three integers as per 'Stringularity', or the first law of theoretical physics.
'Self-referentially' this feeds back between zero and ‘Phi’ or 0.618 and from this one might say the 'origin' & derivation of 'Phi' if profound, are not quite so 'mysterious' after all.
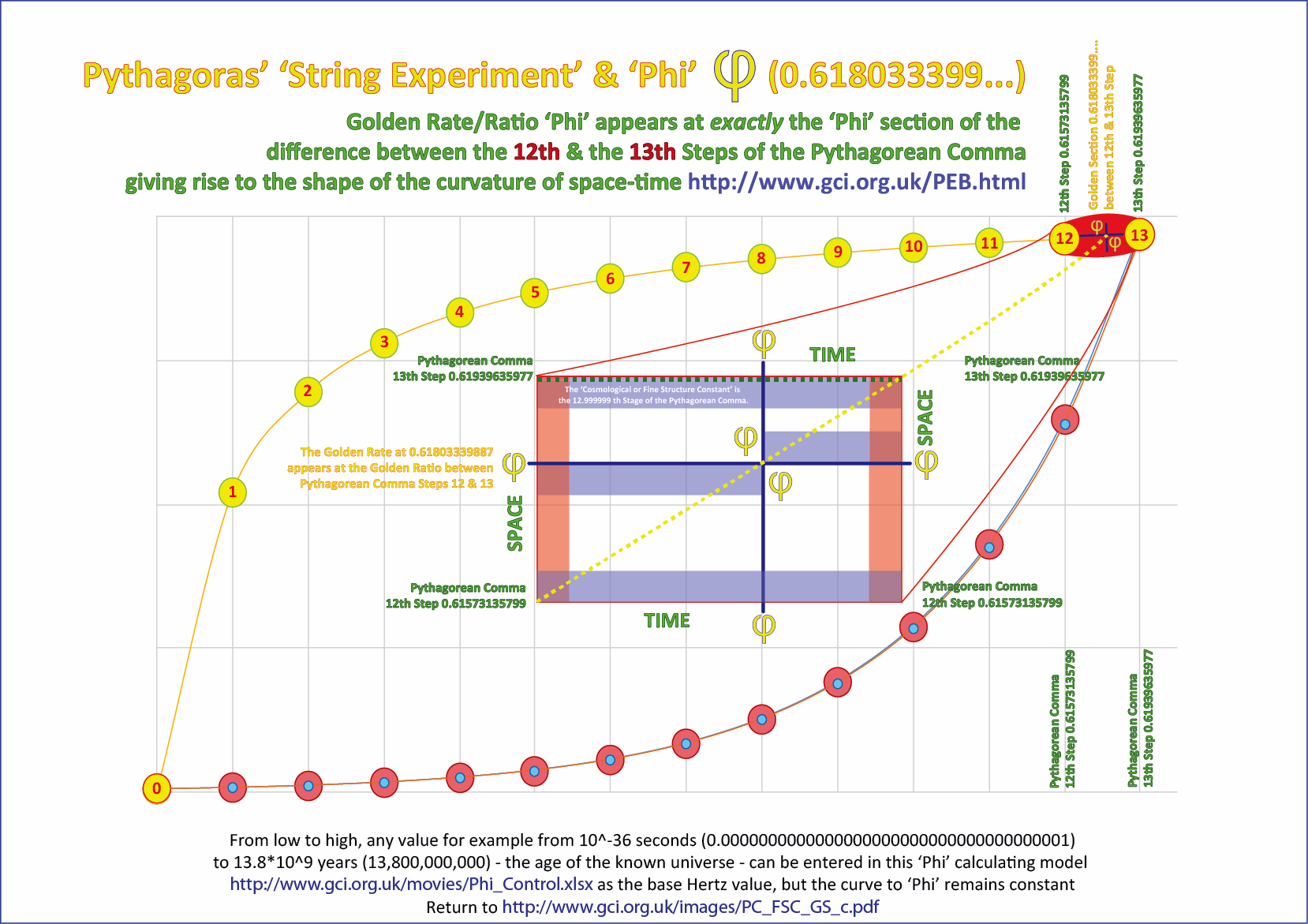
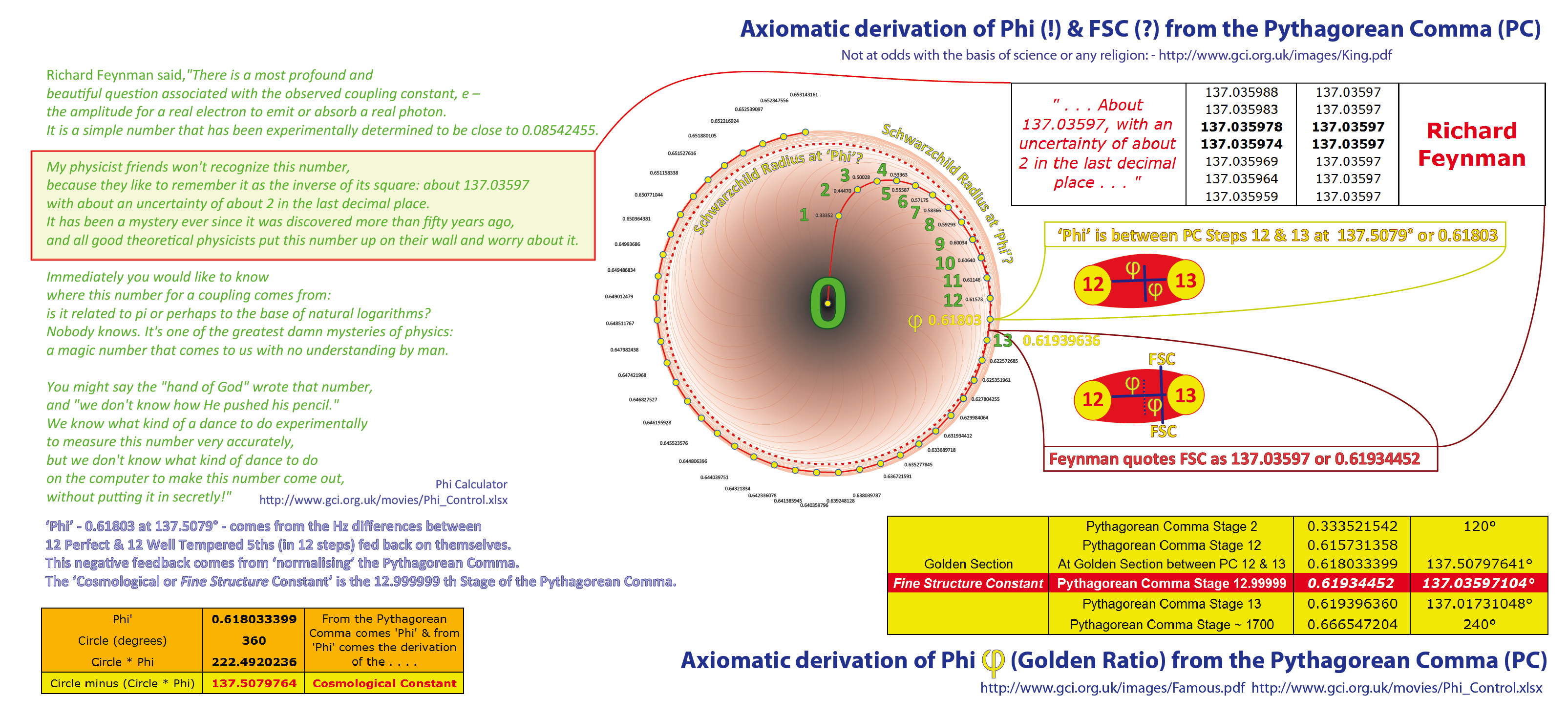
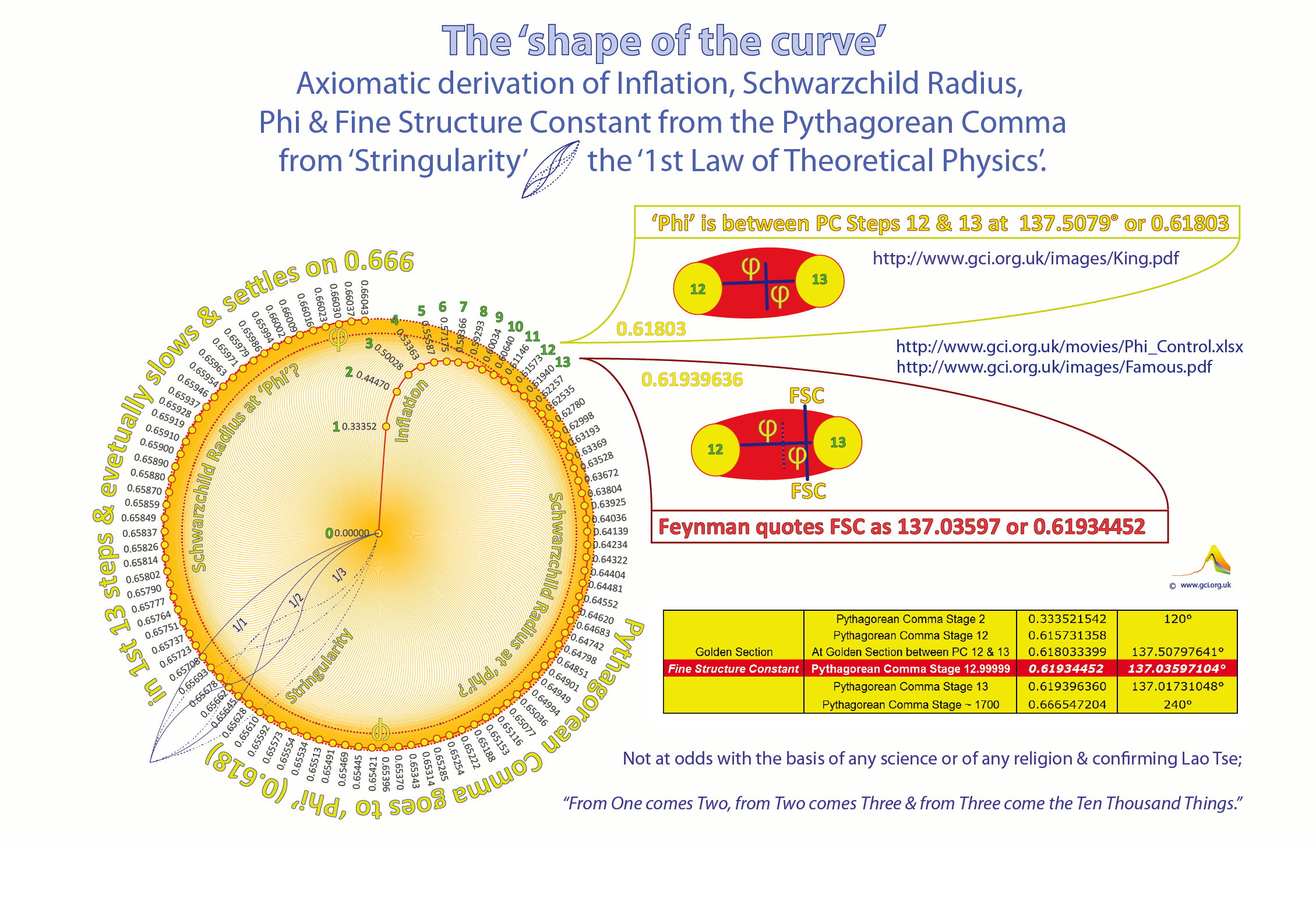
The precise position of 'Phi' - on what Chis Hope has appropriately called 'the musical curve' - is between the 12th & the 13th steps of the emergence of the Pythagorean Comma -
exactly & exquisitely at the 'Phi' position on that segement of the curve (as shown in the chart below).
Another image of the 'Phi-Position' between the 12th & the 13th steps of the Pythagorean Comma.
The calculating spreadsheets are here
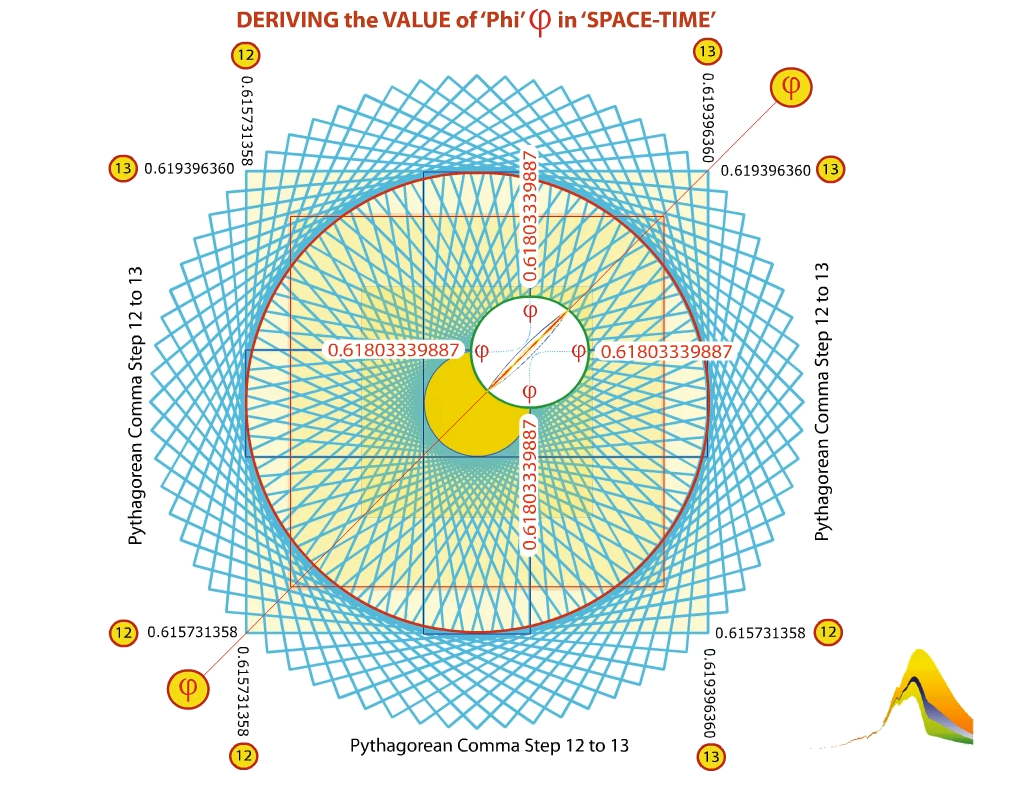
Another image of the 'Phi-Position' between the 12th & the 13th steps of the Pythagorean Comma
Click the image . . .
Then there is the fascinating matter of where the so-called 'Cosmological Constant' exists in relation to Phi. Phi is at 137.5079° or 0.61803.... the value for the 'Fine Structure Constant' quoted by Richard Feynman is at 137.03957 or 0.61934452. Though the precise value of FSC is still debated, even to the extent that it is not always strictly regarded as even exactly 'constant', 'Phi' and the rate of its derivation is certainly axiomatically constant. That said they are very close and both are contained precisely between the 12th and 13th steps of the Pythagorean Comma.They are not 'identical' but the are very close. Also, if the Phi position emerged 'arithmetically' at the inflationary moment after the the big bang, the FSC may not be quite 'constant' as it is being measured on today's photon/electron exchange 13.8 Billion years later, in a universe that has been expanding since inflation and where 'the musical curve' itself has been expanding but decelerating very gradually from 0.618 to 0.666 (as shown in the charts below).
Electro-magnetically, the influence of ‘Phi’ is evident throughout nature at every scale of time & space. This evidence of 'Phi' is often seen, heard and felt as 'awe-inspiring'. From the spiral of galaxies to the double helix of DNA, 'Phi' is dynamically encoded in the simple, subtle, self-structuring and self-limiting growth patterns of sunflower seeds, pineapples, fir cones, the human cochlea - in a phrase it is axiomatically encoded in Nature at all scales.
All from the 'Hemiola' - truly awe-inspiring . . .
From zero to one; so what really happened at the Big Bang?
Another view of the evolution of 'Phi', here plotted on a 'radar' chart.And another (click image to get full screen - zoomable for detail)
A user-chooser Phi at any scale 'calculator' is here
At the core 'Phi' and the First Law of 'non'-theoretical physics is the source of all we have: -
The derivation of Phi; Pi:Phi equivalence and how this generates the double helix structure of DNA
Some people ask, "what has music got to do with climate change?"
Perhaps instead one can ask, are ‘Stringularity' and the Golden Rate/Ratio what drive musicians and especially perhaps string-playing musicians,
to measure the fine structure of frequency governed this way with such minute accuracy?The ‘living music of Phi-the-rate’ that emerges from ‘Stringularity’, is key to the resilience of ‘the Well-Tempered Climate Accord’,
the 'CBAT' methodology for collective global action to cut carbon emissions in time to keep in tune with the planet,
other life-forms and ourselves, failing which a catastrophe looms (Sir David King)Often known as ‘Contraction & Convergence’ (C&C), C&C is embedded as Domain Two in 'CBAT', the 'Carbon Budget Analysis Tool'.
Support for CBAT has been considerable. Another recent example is "Escape from Overshoot" by Peter A Victor.
After thirty years this Well-Tempered 'C&C-methodology' remains robust,
widely supported and unchallenged at a fundamental level.
360/1.618 = 222.4969
360-222.4969=137.5013Portmeirion Festival Presentation 03 09 2016
(Come to where the two rivers meet)Richard Feynman, one of the originators and early developers of the theory of quantum electrodynamics (QED), referred to the fine-structure constant in these terms:
"There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon.
It is a simple number that has been experimentally determined to be close to 0.08542455.My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place.
It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms?
Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man.You might say the "hand of God" wrote that number, and "we don't know how He pushed his pencil."
We know what kind of a dance to do experimentally to measure this number very accurately,
but we don't know what kind of dance to do on the computer to make this number come out,
without putting it in secretly!"Richard Feynman, Richard P. Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. p. 129. ISBN 0-691-08388-6.
Well Tempering & the musical derivation of the wonderous 'Phi' (0.618)
- Phi Derivation Model - 'The Stringularity Hypothesis'
- Hawking drew short of recognizing the real significance of Pythagoras String Experiment
- The symmetry-binding-derivation of 'Phi' from the Pythagorean Comma
- Symmetry-binding at the Phi-Point between steps 12 & 13 of the Pythagorean Comma
- Precise close-up of 'Phi' at the 'Phi-Point' between steps 12 & 13 of the Pythgorean Comma
- Symmetry-binding derivation of Phi rescues Standard-Model when Higgs Particle is added
- The Feminine Principle
- Phi-rich Pentagons
- Phi created the integers
- Happy Phi:Pi Day
- Phi at Green in visble Colour Spectrum & beautiful 'Fluminescence' from Ginny Battson
- Phi All Life
- Phi:Pi - governs orbits of Earth Venus and Sun
- Phi:Pi - governs DNA double-helix molecule
- Phi is at the structural core of DNA
- Equivalence
- Certainty in the derivation of Phi, the structure of DNA, Rosalind Franklin & Choose Life
- Phi:Pi - Khufu
- Phi:Pi - Squaring the Circle
- Phi:Pi - Schwarzchild Radius
- Hemiola
- Deep Simplicity
- Eternity & golden spiralling electrons/'excitons'
- A Beautiful Model (Limits to Growth)
- Awesome Sunrise
- Inside Out outside In for fun . . . . .